This function creates a Relative Weights Analysis (RWA) and
returns a list of outputs. RWA provides a heuristic method for estimating
the relative weight of predictor variables in multiple regression, which
involves creating a multiple regression with on a set of transformed
predictors which are orthogonal to each other but maximally related to the
original set of predictors. rwa() is optimised for dplyr pipes and shows
positive / negative signs for weights.
Usage
rwa(
df,
outcome,
predictors,
applysigns = FALSE,
method = "auto",
sort = TRUE,
bootstrap = FALSE,
n_bootstrap = 1000,
conf_level = 0.95,
focal = NULL,
comprehensive = FALSE,
include_rescaled_ci = FALSE
)Arguments
- df
Data frame or tibble to be passed through.
- outcome
Outcome variable, to be specified as a string or bare input. Must be a numeric variable.
- predictors
Predictor variable(s), to be specified as a vector of string(s) or bare input(s). All variables must be numeric.
- applysigns
Logical value specifying whether to show an estimate that applies the sign. Defaults to
FALSE.- method
String to specify the method of regression to apply. Valid values include:
"auto": automatically detect whether to use multiple regression or logistic regression based on the outcome variable provided."multiple": use multiple regression."logistic": use logistic regression.
- sort
Logical value specifying whether to sort results by rescaled relative weights in descending order. Defaults to
TRUE.- bootstrap
Logical value specifying whether to calculate bootstrap confidence intervals. Defaults to
FALSE. Currently only supported for multiple regression.- n_bootstrap
Number of bootstrap samples to use when bootstrap = TRUE. Defaults to 1000.
- conf_level
Confidence level for bootstrap intervals. Defaults to 0.95.
- focal
Focal variable for bootstrap comparisons (optional).
- comprehensive
Whether to run comprehensive bootstrap analysis including random variable and focal comparisons.
- include_rescaled_ci
Logical value specifying whether to include confidence intervals for rescaled weights. Defaults to
FALSEdue to compositional data constraints. Use with caution.
Value
rwa() returns a list of outputs, as follows:
predictors: character vector of names of the predictor variables used.rsquare: the rsquare value of the regression model (multiple regression only).result: the final output of the importance metrics (sorted by Rescaled.RelWeight in descending order by default).The
Rescaled.RelWeightcolumn sums up to 100.The
Signcolumn indicates whether a predictor is positively or negatively correlated with the outcome.When bootstrap = TRUE, includes confidence interval columns for raw weights.
Rescaled weight CIs are available via include_rescaled_ci = TRUE but not recommended for inference.
n: indicates the number of observations used in the analysis.bootstrap: bootstrap results (only present when bootstrap = TRUE), containing:ci_results: confidence intervals for weightsboot_object: raw bootstrap object for advanced analysisn_bootstrap: number of bootstrap samples used
lambda: lambda matrix from the RWA calculation.RXX: Correlation matrix of all the predictor variables against each other. Not available for logistic regression.RXY: Correlation values of the predictor variables against the outcome variable. Not available for logistic regression.
Details
rwa() produces raw relative weight values (epsilons) as well as rescaled
weights (scaled as a percentage of predictable variance) for every predictor
in the model. Signs are added to the weights when the applysigns argument
is set to TRUE. See https://www.scotttonidandel.com/rwa-web for the
original implementation that inspired this package.
This function is a wrapper around rwa_multiregress() and rwa_logit(),
automatically selecting the appropriate method based on the outcome variable
or the method argument.
See also
plot_rwa() for plotting results, rwa_multiregress() and
rwa_logit() for the underlying implementations.
Examples
library(ggplot2)
# Basic RWA (results sorted by default)
rwa(diamonds, "price", c("depth", "carat"))
#> Parsing `price` as a non-binary variable.
#> Applying multiple regression to calculate relative weights...
#> $predictors
#> [1] "depth" "carat"
#>
#> $rsquare
#> [1] 0.8506755
#>
#> $result
#> Variables Raw.RelWeight Rescaled.RelWeight Sign
#> 1 carat 0.849946308 99.91428588 +
#> 2 depth 0.000729149 0.08571412 -
#>
#> $n
#> [1] 53940
#>
#> $lambda
#> [,1] [,2]
#> [1,] 0.99990040 0.01411356
#> [2,] 0.01411356 0.99990040
#>
#> $RXX
#> depth carat
#> depth 1.00000000 0.02822431
#> carat 0.02822431 1.00000000
#>
#> $RXY
#> depth carat
#> -0.0106474 0.9215913
#>
# RWA without sorting (preserves original predictor order)
rwa(diamonds, "price", c("depth", "carat"), sort = FALSE)
#> Parsing `price` as a non-binary variable.
#> Applying multiple regression to calculate relative weights...
#> $predictors
#> [1] "depth" "carat"
#>
#> $rsquare
#> [1] 0.8506755
#>
#> $result
#> Variables Raw.RelWeight Rescaled.RelWeight Sign
#> 1 depth 0.000729149 0.08571412 -
#> 2 carat 0.849946308 99.91428588 +
#>
#> $n
#> [1] 53940
#>
#> $lambda
#> [,1] [,2]
#> [1,] 0.99990040 0.01411356
#> [2,] 0.01411356 0.99990040
#>
#> $RXX
#> depth carat
#> depth 1.00000000 0.02822431
#> carat 0.02822431 1.00000000
#>
#> $RXY
#> depth carat
#> -0.0106474 0.9215913
#>
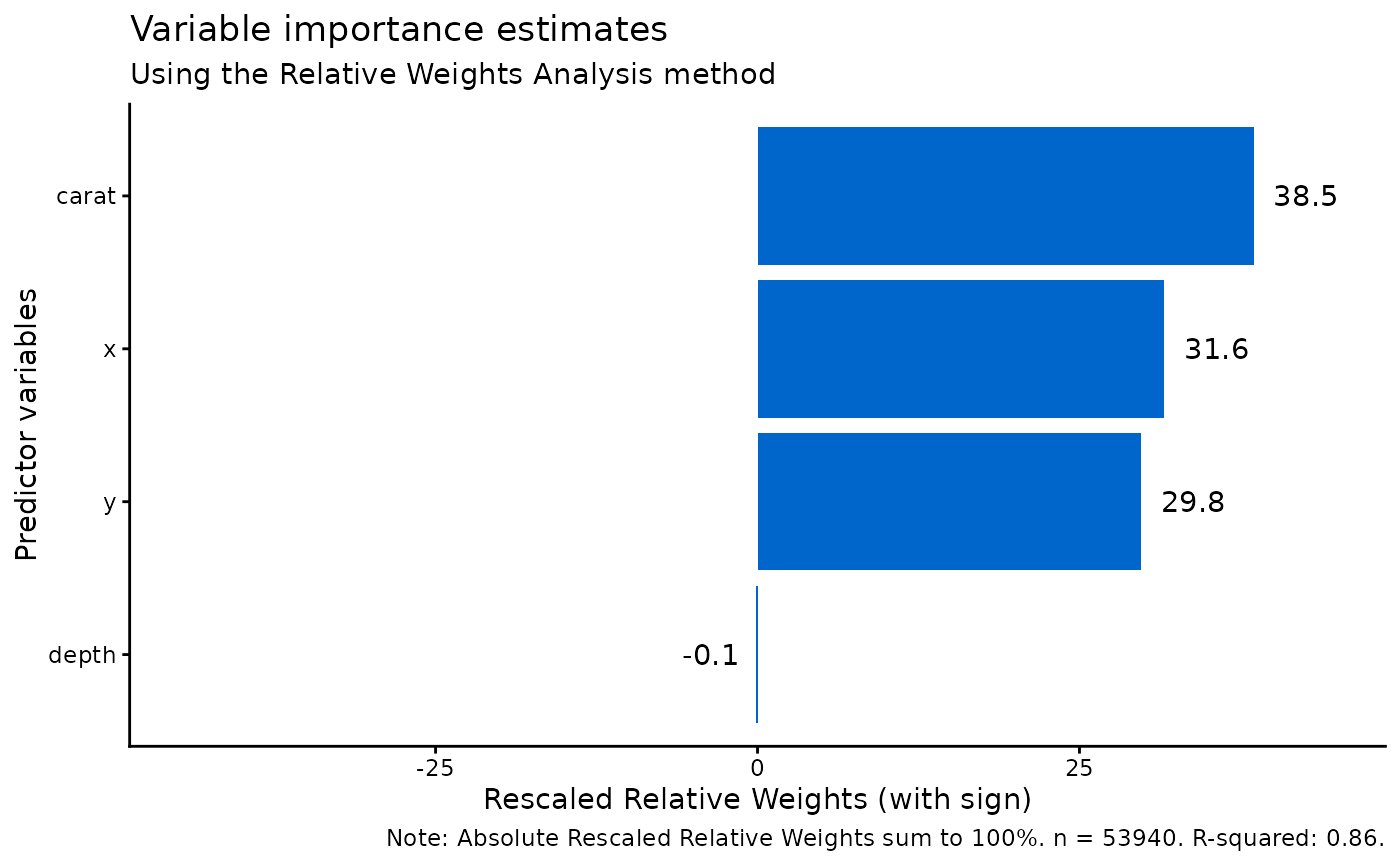
# Plot results using plot_rwa()
diamonds |>
rwa("price", c("depth", "carat", "x", "y")) |>
plot_rwa()
#> Parsing `price` as a non-binary variable.
#> Applying multiple regression to calculate relative weights...
# \donttest{
# For faster examples, use a subset of data for bootstrap
diamonds_small <- diamonds[sample(nrow(diamonds), 1000), ]
# RWA with bootstrap confidence intervals (raw weights only)
rwa(diamonds_small, "price", c("depth", "carat"),
bootstrap = TRUE, n_bootstrap = 100)
#> Parsing `price` as a non-binary variable.
#> Applying multiple regression to calculate relative weights...
#> Running bootstrap analysis with 100 samples...
#> $predictors
#> [1] "depth" "carat"
#>
#> $rsquare
#> [1] 0.8499131
#>
#> $result
#> Variables Raw.RelWeight Rescaled.RelWeight Sign Raw.RelWeight.CI.Lower
#> 1 carat 0.8489637953 99.8883007 + 0.821172909
#> 2 depth 0.0009493473 0.1116993 - -0.002577354
#> Raw.RelWeight.CI.Upper Raw.Significant
#> 1 0.878932350 TRUE
#> 2 0.001598172 FALSE
#>
#> $n
#> [1] 1000
#>
#> $lambda
#> [,1] [,2]
#> [1,] 0.9998984 0.0142579
#> [2,] 0.0142579 0.9998984
#>
#> $RXX
#> depth carat
#> depth 1.0000000 0.0285129
#> carat 0.0285129 1.0000000
#>
#> $RXY
#> depth carat
#> -0.01473139 0.92099482
#>
#> $bootstrap
#> $bootstrap$boot_object
#>
#> ORDINARY NONPARAMETRIC BOOTSTRAP
#>
#>
#> Call:
#> boot::boot(data = bootstrap_data, statistic = rwa_boot_statistic,
#> R = n_bootstrap, outcome = outcome, predictors = predictors)
#>
#>
#> Bootstrap Statistics :
#> original bias std. error
#> t1* 0.0009493473 0.0006083043 0.001005676
#> t2* 0.8489637953 -0.0009349687 0.014284910
#>
#> $bootstrap$ci_results
#> $bootstrap$ci_results$raw_weights
#> # A tibble: 2 × 6
#> variable weight_index ci_lower ci_upper ci_method ci_type
#> <chr> <int> <dbl> <dbl> <chr> <chr>
#> 1 depth 1 -0.00258 0.00160 basic raw
#> 2 carat 2 0.821 0.879 basic raw
#>
#>
#> $bootstrap$n_bootstrap
#> [1] 100
#>
#> $bootstrap$conf_level
#> [1] 0.95
#>
#> $bootstrap$comprehensive
#> [1] FALSE
#>
#> $bootstrap$focal
#> NULL
#>
#>
# Include rescaled weight CIs (use with caution for inference)
rwa(diamonds_small, "price", c("depth", "carat"),
bootstrap = TRUE, include_rescaled_ci = TRUE, n_bootstrap = 100)
#> Parsing `price` as a non-binary variable.
#> Applying multiple regression to calculate relative weights...
#> Running bootstrap analysis with 100 samples...
#> Warning: Rescaled weight confidence intervals should be interpreted with caution due to compositional data constraints. Use for descriptive purposes only, not formal statistical inference.
#> $predictors
#> [1] "depth" "carat"
#>
#> $rsquare
#> [1] 0.8499131
#>
#> $result
#> Variables Raw.RelWeight Rescaled.RelWeight Sign Raw.RelWeight.CI.Lower
#> 1 carat 0.8489637953 99.8883007 + 0.820116111
#> 2 depth 0.0009493473 0.1116993 - -0.001621699
#> Raw.RelWeight.CI.Upper Raw.Significant Rescaled.RelWeight.CI.Lower
#> 1 0.874260240 TRUE 99.8007012
#> 2 0.001587324 FALSE -0.2253907
#> Rescaled.RelWeight.CI.Upper
#> 1 100.2253907
#> 2 0.1992988
#>
#> $n
#> [1] 1000
#>
#> $lambda
#> [,1] [,2]
#> [1,] 0.9998984 0.0142579
#> [2,] 0.0142579 0.9998984
#>
#> $RXX
#> depth carat
#> depth 1.0000000 0.0285129
#> carat 0.0285129 1.0000000
#>
#> $RXY
#> depth carat
#> -0.01473139 0.92099482
#>
#> $bootstrap
#> $bootstrap$boot_object
#>
#> ORDINARY NONPARAMETRIC BOOTSTRAP
#>
#>
#> Call:
#> boot::boot(data = bootstrap_data, statistic = rwa_boot_statistic,
#> R = n_bootstrap, outcome = outcome, predictors = predictors)
#>
#>
#> Bootstrap Statistics :
#> original bias std. error
#> t1* 0.0009493473 0.0006033209 0.0009143211
#> t2* 0.8489637953 0.0037448894 0.0127520755
#>
#> $bootstrap$boot_object_rescaled
#>
#> ORDINARY NONPARAMETRIC BOOTSTRAP
#>
#>
#> Call:
#> boot::boot(data = bootstrap_data, statistic = rwa_boot_statistic_rescaled,
#> R = n_bootstrap, outcome = outcome, predictors = predictors)
#>
#>
#> Bootstrap Statistics :
#> original bias std. error
#> t1* 0.1116993 0.05818349 0.1031148
#> t2* 99.8883007 -0.05818349 0.1031148
#>
#> $bootstrap$ci_results
#> $bootstrap$ci_results$raw_weights
#> # A tibble: 2 × 6
#> variable weight_index ci_lower ci_upper ci_method ci_type
#> <chr> <int> <dbl> <dbl> <chr> <chr>
#> 1 depth 1 -0.00162 0.00159 basic raw
#> 2 carat 2 0.820 0.874 basic raw
#>
#> $bootstrap$ci_results$rescaled_weights
#> # A tibble: 2 × 6
#> variable weight_index ci_lower ci_upper ci_method ci_type
#> <chr> <int> <dbl> <dbl> <chr> <chr>
#> 1 depth 1 -0.225 0.199 basic rescaled
#> 2 carat 2 99.8 100. basic rescaled
#>
#>
#> $bootstrap$n_bootstrap
#> [1] 100
#>
#> $bootstrap$conf_level
#> [1] 0.95
#>
#> $bootstrap$comprehensive
#> [1] FALSE
#>
#> $bootstrap$focal
#> NULL
#>
#>
# Comprehensive bootstrap analysis with focal variable
result <- rwa(diamonds_small, "price", c("depth", "carat", "table"),
bootstrap = TRUE, comprehensive = TRUE, focal = "carat",
n_bootstrap = 100)
#> Parsing `price` as a non-binary variable.
#> Applying multiple regression to calculate relative weights...
#> Running bootstrap analysis with 100 samples...
# View confidence intervals
result$bootstrap$ci_results
#> $raw_weights
#> # A tibble: 3 × 6
#> variable weight_index ci_lower ci_upper ci_method ci_type
#> <chr> <int> <dbl> <dbl> <chr> <chr>
#> 1 depth 1 -0.00147 0.00180 basic raw
#> 2 carat 2 0.817 0.872 basic raw
#> 3 table 3 -0.00381 0.0148 basic raw
#>
#> $random_comparison
#> # A tibble: 3 × 6
#> variable weight_index ci_lower ci_upper ci_method ci_type
#> <chr> <int> <dbl> <dbl> <chr> <chr>
#> 1 Var4 1 -0.00134 0.00416 basic rand_diff
#> 2 Var5 2 0.816 0.870 basic rand_diff
#> 3 Var6 3 -0.00120 0.0156 basic rand_diff
#>
#> $focal_comparison
#> # A tibble: 2 × 6
#> variable weight_index ci_lower ci_upper ci_method ci_type
#> <chr> <int> <dbl> <dbl> <chr> <chr>
#> 1 Var7 1 -0.869 -0.813 basic focal_diff
#> 2 Var8 2 -0.865 -0.805 basic focal_diff
#>
# }
# Based on logistic regression (auto-detected from binary outcome)
diamonds$IsIdeal <- as.numeric(diamonds$cut == "Ideal")
rwa(diamonds, "IsIdeal", c("depth", "carat"))
#> Parsing `IsIdeal` as a binary variable.
#> Applying logistic regression to calculate relative weights...
#> $predictors
#> [1] "depth" "carat"
#>
#> $rsquare
#> [1] 0.02835802
#>
#> $result
#> Variables Raw.RelWeight Rescaled.RelWeight Sign
#> 1 carat 0.0279360368 98.511958 -
#> 2 depth 0.0004219793 1.488042 -
#>
#> $n
#> [1] 53940
#>
#> $lambda
#> depth carat
#> [1,] 0.99990040 0.01411356
#> [2,] 0.01411356 0.99990040
#>